Practical Parallel Computing

Parallel computing is a form of computation in which many calculations are carried out simultaneously. This is almost the only way of taking full power of today’s computers.

CPU have reached the point where it is not possible to increase the frequency of operation. The only way to increase computation power is to multiply the CPU. Either fully using multi-CPU computer, or partially using multi-core and hyper threading.

Most of today’s PC are equipped with 4 cores CPU. High end workstations have multiple CPU each with multiple cores and even hyper threading. For example, my own computer is a HP Z600 workstation having two Intel Xeon processors each one having 4 cores and hyper threading. Using Windows task manager, you actually see 16 processors.

Not an easy task

To benefit from multi cores computers, you must write programs so that the problem is divided into smaller ones which are then executed in parallel.

Not all problems can be divided in smaller ones for parallel execution. Numerical computation is one domain where parallelism is often possible. In this article, I will show the programming for a heavy computing problem: exploring the Mandelbrot set. Mandelbrot set is well known. It is mostly shown as a beautiful colorful picture which may take a very long time to compute. Using parallel computing will result in a high performance gain provided you run on a modern computer.

Parallel computer programs are more difficult to write than sequential ones, because concurrency introduces several new classes of potential software bugs.

The most common concurrency problem is when one task writes some shared data which is read by another task. If nothing special is done, then the reader may read partial data! The writer starts writing following data while the reader has not finished reading previous data. This kind of bug is difficult to find because it does not always occur. It depends on how one task runs compared to other task. This is referred as a race condition. Most of the time, it works because the reading and writing are occurring at different times. Sometimes it does not work because reading and writing overlaps.

Multithreading

Multithreading is the way you write parallel programs using traditional languages such as C/C++, Delphi or C# running on traditional (PC) computers. Other languages or other hardware architecture exists, but this is beyond of this article which is related to PC programming.

A thread is an execution path managed by an operating system. Multiple threads are executed simultaneously by a processor when the processor has multiple cores. With a single core processor, you still have multithreading, but they are executed one after the other. Execution switches quickly between each thread, making the human eye see all executing in parallel. They are really executed in parallel with multi core CPU or when multiple CPU are available.

It is the operating system and the language run time that take care of the required housekeeping. As seen from the programming language, a thread looks mostly like a simple function call (or an object’s method call when using an object oriented language). The difference with a normal function call is that when using multithreading, the function returns immediately while the function’s code is executed in parallel with the caller’s code.

Synchronization

To avoid messing everything, the work accomplished by different threads has to be synchronized.

For example, data cannot be read while it is being written by another thread. Several threads can simultaneously read the same data, but when one is writing data, it must be the only one accessing the data.

Another example is computing. Adding a value to a variable must be executed by a thread having exclusive access to that data. This is, at another level, the same issue as we find in multiple user database application. In such application, we use a “record lock” so that a record can be read, some computation done and then written back in an atomic operation. That is, no other user can have access to the data while the first reads-computes-writes.

The very same problem exists with multithreading. Simply the data is not in a database but in memory. Every single variable has to be protected from simultaneous reading and writing. And some operations, such as adding a variable to another one must be done atomically. And by the way, if multiple threads are doing database access, we have to use the exact same “record lock” as we do for a multiple user application.

A last example: frequently, when a problem is divided in multiple parts for parallel execution, something must be done at one point in time to be sure that all parts are done before continuing. Imagine you use parallel processing to create a dataset in memory. You must wait until all threads are done before writing the result to the file.

Operating system and language runtime provide many synchronization mechanisms. For example: critical section, semaphore, mutex, queues and others.

Introduction to Mandelbrot set

Benoît Mandelbrot, who died on 10/14/2010, was a famous mathematician. He studied fractal geometry. He found that chaos can emerge from a very simple equation:

This equation is iteration where c is a constant. We start from a first value X0 and compute X1 using the formula. Using X1 we then compute X2 and so on. This is no fun but easy. Where it becomes interesting is when we do this calculation using complex numbers and when we look what happens after a lot of iterations. Depending on the constant c, we can see that the Xn value increases quickly or not. Sometimes, the value change but never become very large. Even if computing a lot of iterations, we cannot decide whether the value will become very large.

Complex numbers can be represented by two numbers forming the coordinates X and Y on a plane. This is exactly what we use to draw a colorful representation of the Mandelbrot set. Each pixel on the image is one value of the constant c in the iteration above. The color of each pixel is given by the number of iterations computed so that the Xn value becomes large. The number of iterations is limited to a maximum. If the maximum is reached, the pixel is colored in a specific color, usually black or white. The result looks like this:

Using Delphi, the code to compute the value of a given point is as follow:

function ComputeMandelPoint(P, Q : Extended; MaxIter : Integer) : Integer;
var
    X0, Y0, X, Y : Extended;
    R, M         : Extended;
    K            : Integer;
begin
    M  := 100;
    K  := 0;
    X0 := 0;
    Y0 := 0;

    while TRUE do begin
        X  := X0 * X0 - Y0 * Y0 + p;
        Y  := 2.0 * X0 * Y0 + q;
        K  := K + 1;

        R := X * X + Y * Y;
        if R > M then
            break
        else if K >= MaxIter then begin
            K := MaxIter + 1;
            break;
        end;
        X0 := X;
        Y0 := Y;
    end;
    Result := K;
end;

In this code, P and Q are the coordinates of one point in the complex plane. The image is computed for P in the range [-2.4 … 1.0] and Q in the range [-1.3 … 1.3] and a maximum number of iterations of 1000. Coloring is done using a continuous palette composed of 48 shades of blue like this:

Since the value of each pixel is 0 to the maximum number of iteration, the palette is used cyclically. An offset of 25 is given so that the white limit is positioned nicely.

The code here above implements the formula we saw earlier. The code layout may looks strange. It has been done like that for speed optimization.

Building an image from the Mandelbrot set

The image showed above is quite easy to obtain. Here is the set of operations
1. Create a bitmap of a given resolution (1024 x 768 pixel for example)
2. Associate each bitmap pixel to the couple P, Q according to the area you want to display. In the image above, X on the bitmap (0..1023) is mapped to P = [-2.4 … 1.0] and Y on the bitmap (0..767) is mapped to Q = [-1.3 … 1.3].
3. Iterate all X, Y on the bitmap to compute the value of the pixel as a number of iterations.
4. Map the pixel value in iteration to the color value according to the color palette you like.

Mapping bitmap pixel to Mandelbrot set point

The process of step 2 above is named “mapping”. In math language, it is a simple coordinate transformation from one coordinate system (bitmap) to another one (Mandelbrot set).

Graphically, we can represent a graphic with one system on the abscissa (horizontal axis) and on the ordinate (vertical axis) we have the other system:

We can express the slope of the line as seen from X, X1, Y, Y1 and from X2, X1, Y2, Y1 which are obviously the same:

We can rewrite this equation to have the Y value based on all others:

Let’s say we want to transform the X coordinate on a bitmap to the equivalent Y coordinate in the Mandelbrot set. For example, on the bitmap shown above we go from pixel 0 to pixel 1023 and on the Mandelbrot set we go from -2.4 on the left to 1.0 on the right. This gives:

X1 = 0, X2 = 1023, Y1 = -2.4, Y2 = 1.0

Now applying our equation, given an arbitrary pixel coordinate X, we can compute the equivalent value in the Mandelbrot set:

Mandel := -2.4 + (Bitmap – 0) * (1.0 - -2.4) / (1023 – 0)

Note that (Y2 – Y1) / (X2 – X1) which is the slope of the line in the above diagram is frequently named zoom factor.

We can do similar computation for the pixel coordinate Y, using the same zoom factor so that the image is not distorted.

If we put all this in a simple Delphi program, we will get the following code:

procedure TMandelSimpleForm.FormShow(Sender: TObject);
var
    Bitmap : TBitmap;
    X, Y   : Integer;
    P, Q   : Extended;
    V      : Integer;
    Slope  : Extended;
    Colors : array of TColor;
    T0     : Cardinal;
const
    MandelLeft   = -2.4;
    MandelRight  = 1.0;
    MandelBottom = -1.3;
    MaxIter      = 1000;
begin
    SetLength(Colors, 11);
    Colors[ 0] := RGB( 47,  47, 255);
    Colors[ 1] := RGB( 21,  21, 255);
    Colors[ 2] := RGB(  0,   0, 255);
    Colors[ 3] := RGB(255, 255, 255);
    Colors[ 4] := RGB(229, 229, 255);
    Colors[ 5] := RGB(203, 203, 255);
    Colors[ 6] := RGB(177, 177, 255);
    Colors[ 7] := RGB(151, 151, 255);
    Colors[ 8] := RGB(125, 125, 255);
    Colors[ 9] := RGB( 99,  99, 255);
    Colors[10] := RGB( 73,  73, 255);

    Bitmap             := TBitmap.Create;
    Bitmap.PixelFormat := TPixelFormat.pf24bit;
    Bitmap.Width       := Image1.Width;
    Bitmap.Height      := Image1.Height;

    Slope := (MandelRight - MandelLeft) / (Bitmap.Width - 1);

    T0 := GetTickCount;
    for Y := 0 to Bitmap.Height - 1 do begin
        for X := 0 to Bitmap.Width - 1 do begin
            P := MandelLeft   + X * Slope;
            Q := MandelBottom + Y * Slope;
            V := ComputeMandelPoint(P, Q, MaxIter);
            Bitmap.Canvas.Pixels[X, Y] := Colors[V mod Length(Colors)];
        end;
    end;
    Image1.Picture.Bitmap := Bitmap;
    T0 := GetTickCount - T0;
    Bitmap.Free;
    ShowMessage('Computed in ' + IntToStr(T0) + ' mS');
end;

This code is really complete. We don’t need more to have a nice Mandelbrot set shown on screen. To create the application, use the following steps:

• Create a new VCL forms application
• Enlarge the form so that a 1024x768 bitmap will fit
• Drop a TImage on the form, make it 1024x768
• Add the code above to the form’s OnShow even.
• Save, compile and run.

On my computer, it takes 4400 mS to build the bitmap. The parallel computing version will run in 690 mS for the same bitmap. This is a 6 fold improvement. It deserves the effort. Those numbers are for a Win32 application. When rebuilt as a Win64 application, times are divided by 2.

Parallel computing of a Mandelbrot set

Overview of required steps:

• Create a large bitmap to hold the full final image of the Mandelbrot set
• Divide the total area into a lot of smaller areas
• Start a number threads giving each one area to compute
• When a thread finishes his area, submit the area for “painting” and give a new area, if any remains
• When there is no more area to give to a thread, terminate the thread
• When all threads are terminated, all areas are computed.
• Since painting is incredibly faster than computing, short after the last thread finishes, the last area is painted and the full bit map is ready

Dividing Mandelbrot set computation in smaller chunks is easy: divide the bitmap into areas and delegate the computing for those areas to a number of threads.

In my Mandelbrot Explorer, I divided the bitmap as 128x128 pixel areas. If the image size is not a multiple of 128x128, then some areas are smaller and may even be a single pixel.

The areas are described by a class instance with all required parameters. All areas are kept in an object list.

Then a number of threads are created, for example 10 threads, and kept in an object list. Each thread receives one area to process. When it has finished processing the assigned area, the next available area is given to the thread. If no more area is available, the thread is terminated, removed from the list and freed.

Each thread computes the number of iterations for each pixel. Coloring is done by the main thread after computation is done. This is interesting because you can change color mapping without computing again. Coloring is quite fast: on my machine, it is almost instantaneous.

Submitting an area for coloring is done using a custom message posted to the message queue. We need to use that technique because submission is executed in the thread’s context and we want the main thread to do the coloring. Using custom messages is an easy way of inter-thread communication.

The code

The class describing each area is as follow:

TMandelArea = class
public
    Rect     : TGPRect;           // Area rectangle in full bitmap
    PixValue : array of Integer;  // Computed pixel value
    Zoom     : Extended;          // To compute (P, Q) from bitmap coord
    XOffset  : Extended;          // To compute (P, Q) from bitmap coord
    YOffset  : Extended;          // To compute (P, Q) from bitmap coord
    Colors   : TList;     // The list of colors for coloring
    MaxIter  : Integer;           // Max iterations when computing
    Index    : Integer;           // Index in areas list
    procedure Compute;            // Compte all pixels in area
    // Colorize the pixel in the area and draw the area into full bitmap
    procedure Colorize(FullBitmap  : IGPBitmap;
                       ColorInside : TColor;
                       ColorDiv    : Integer;
                       ColorOff    : Integer);
end;

TMandelArea is a very simple class. It has all the fields with parameters we talked about and two methods. One for computing the pixel values and one for colorize the pixels and transfer the result in the full bitmap.

What I named “FullBitmap” is an interface coming from GDI+. Windows GDI+ is a class-based API that provides two-dimensional vector graphics, imaging, and typography. It is faster than Windows GDI API which is used by Delphi runtime.

TMandelArea.Compute is quite trivial. It looks much like the method we have seen above in the simple Mandelbrot application. Here it is:

procedure TMandelArea.Compute;
var
    X, Y       : Integer;
    P, Q       : Extended;
    Index      : Integer;
begin
    SetLength(PixValue, Rect.Width * Rect.Height);
    Index := 0;
    for Y := 0 to Rect.Height - 1 do begin
        Q := (Y + Rect.Y) / Zoom + YOffset;
        for X := 0 to Rect.Width - 1 do begin
            P := (X + Rect.X) / Zoom + XOffset;
            PixValue[Index] := ComputeMandelPoint(P, Q, MaxIter);
            Inc(Index);
        end;
    end;
end;

Basically, the method just iterates thru all pixels in the area, transforms the coordinates from bitmap system to Mandelbrot set system and calls the function we have seen above to compute the pixel value. That value is stored in an array of integer. PixValue array is dimensioned before computing.

Computation has nothing to do with creating the result bitmap and coloring its pixels. The resulting bitmap, which will be shown on screen and saved to disk as JPEG, is created before anything else. I use a GDI+ bitmap which is handled thru in interface.

The programmer can access the data of a GDI+ bitmap. For that, it has to call “LockBits” which returns a record having among other things the pointer to actual bitmap data. For better performance, the lines of a bitmap data is always aligned to memory locations. See how Row is calculated below to see how to handle that.

Bitmap data is organized as RGB value, that is 3 bytes for red, green and blue components of each pixel color. In Delphi, a TColor is simply an integer value with the 3 bytes. This is why you see code like: Row^ := Byte(ColorValue shr 16) to extract one of the bytes and copy it to the bitmap memory.

procedure TMandelArea.Colorize(
    FullBitmap  : IGPBitmap;
    ColorInside : TColor;
    ColorDiv    : Integer;
    ColorOff    : Integer);
var
    BitmapData : TGPBitmapData;
    X, Y       : Integer;
    Row        : PByte;
    ColorValue : TColor;
    PixIndex   : Integer;
begin
    BitmapData := FullBitmap.LockBits(Rect, [ImageLockModeWrite],
                                      FullBitmap.PixelFormat);
    PixIndex := 0;
    for Y := 0 to Rect.Height - 1 do begin
        Row := PByte(BitmapData.Scan0) + (Y * BitmapData.Stride);
        for X := 0 to Rect.Width - 1 do begin
            ColorValue := ColorMandelPoint(PixValue[PixIndex],
                                           MaxIter,
                                           ColorInside,
                                           FALSE, 0,
                                           TRUE,
                                           ColorDiv,
                                           ColorOff,
                                           Colors);
            Row^ := Byte(ColorValue shr 16);
            Inc(Row);
            Row^ := Byte(ColorValue shr 8);
            Inc(Row);
            Row^ := Byte(ColorValue);
            Inc(Row);
            Inc(PixIndex);
        end;
    end;
    FullBitmap.UnlockBits(BitmapData);
end;

The thread class:

TMandelThread = class(TThread)
strict private
    FArea       : TMandelArea;
    FNewArea    : TMandelArea;
    FOnComputed : TComputedEvent;
public
    procedure Execute; override;
    property Area       : TMandelArea    read  FArea
                                         write FArea;
    property OnComputed : TComputedEvent read  FOnComputed
                                         write FOnComputed;
end;

implementation

procedure TMandelThread.Execute;
begin
    while Assigned(FArea) do begin
        FArea.Compute;
        FNewArea := nil;
        if Assigned(FOnComputed) then
            FOnComputed(Self, FArea, FNewArea);
        FArea := FNewArea;
    end;
end;

This thread class is incredibly straightforward. It has a single property “Area” which is the area to be computed, a single event “OnComputed” to be called when computation is done and one method “Execute” which is the thread’s entry point.

Execute method is a loop calling Compute method on behalf of the area to be computed and then trigger the OnComputed event to request the next area to compute. The event passes the current computed area (which will be submitted for coloring) and receives, as a var parameter, the new area to compute. If no new area is available, it receives a nil value and the thread terminates the loop.

The main code

The main code must create all the areas, all the threads, allocate areas to threads, colorize areas when computed by each thread and render the result on screen optionally saving it to a jpeg file.

Of course the main code also handles the user interface. I built a nice user interface to help the user explore the Mandelbrot set. I will not describe it here because it is just simple and easy user interface programming.

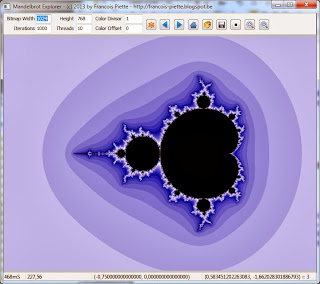
I will just show and describe the user interface:

The tool bar has edit fields to select the bitmap size, the maximum number of iteration, the number of threads to use for computation and color divisor and offset for coloring.

The buttons are to start computing, navigate to previous position, navigate to the next position, show the full Mandelbrot set, change the color palette, save the bitmap to disk file, change the inside color, zoom in and zoom out.

Using the mouse, the user may draw a rectangular area which is then computed. A double click anywhere on the bitmap recomputes a new bitmap centered on the double click point.

On the status bar, you see the time required computing the displayed image, the zoom factor, the coordinates of the image center and the cursor position coordinates with number of iterations at that point.

When the window is resized, the bitmap is as well. The screen always shows the complete bitmap, even if you select a very large bitmap.

If you load a new color palette, the bitmap is colored without computing again. This is almost instantaneous, even on large bitmaps.

The most interesting parts of the code are the method “MandelCreateImage” and the two event handlers for the thread.

procedure TMandelbrotExplorerForm.MandelCreateImage;
var
    Graphics  : IGPGraphics;
    Area      : TMandelArea;
    X, Y      : Cardinal;
    I         : Integer;
    NewThread : TMandelThread;
begin
    // Just do nothing if already terminating
    if FTerminate then
        Exit;

    // We cannot create a new image if threads are still computing
    // We set a flag so that no new area are given to thread and
    // defer processing until all threads are done
    if FThread.Count > 0 then begin
        FTerminate := TRUE;
        PostMessage(Handle, WM_TERMINATING, 0, 0);
        Exit;
    end;

    // Get parameters from user interface, use existing if invalid values
    FMaxIter         := StrToIntDef(MaxIterEdit.Text,  FMaxIter);
    FMandelWidth     := StrToIntDef(WidthEdit.Text,    FMandelWidth);
    FMandelHeight    := StrToIntDef(HeightEdit.Text,   FMandelHeight);
    FThreadCount     := StrToIntDef(ThreadsEdit.Text,  FThreadCount);

    // Validate all parameters
    if FMaxIter < 1 then
        FMaxIter := 1;
    if FMandelWidth < 1 then
        FMandelWidth := 1;
    if FMandelHeight < 1 then
        FMandelHeight := 1;
    if FThreadCount < 1 then
        FThreadCount := 1;

    // Send values back to user interface to replace invalid values
    MaxIterEdit.Text  := IntToStr(FMaxIter);
    WidthEdit.Text    := IntToStr(FMandelWidth);
    HeightEdit.Text   := IntToStr(FMandelHeight);
    ThreadsEdit.Text  := IntToStr(FThreadCount);

    FXOffset          := FCenter.X - (FMandelWidth div 2) / FZoom;
    FYOffset          := FCenter.Y - (FMandelHeight div 2) / FZoom;

    FFullBitmap       := TGPBitmap.Create(FMandelWidth, FMandelHeight,
                                          PixelFormat24bppRGB);
    FBackBrush        := TGPSolidBrush.Create(
                                 TGPColor.Create(GetRValue(clSilver),
                                                 GetGValue(clSilver),
                                                 GetBValue(clSilver)));
    Graphics          := TGPGraphics.FromImage(FFullBitmap);
    Graphics.FillRectangle(FBackBrush,
                           0, 0,
                           FFullBitmap.Width, FFullBitmap.Height);
    // Divide the image into AreaSize x AreaSize pixels
    FAreas.Clear;
    Y := 0;
    while Y < FFullBitmap.Height do begin
        X := 0;
        while X < FFullBitmap.Width do begin
            Area             := TMandelArea.Create;
            Area.Index       := FAreas.Add(Area);
            Area.Colors      := FColors;
            Area.MaxIter     := FMaxIter;
            Area.Zoom        := FZoom;
            Area.XOffset     := FXOffset;
            Area.YOffset     := FYOffset;
            Area.Rect.X      := X;
            Area.Rect.Y      := Y;
            Area.Rect.Width  := Min(AREA_SIZE, FFullBitmap.Width - X);
            Area.Rect.Height := Min(AREA_SIZE, FFullBitmap.Height - Y);
            // Make last rectangle on row or column has correct size
            if (Area.Rect.X + Area.Rect.Width) >= Integer(FFullBitmap.Width) then
                 Area.Rect.Width := Integer(FFullBitmap.Width) - Area.Rect.X;
            if (Area.Rect.Y + Area.Rect.Height) >= Integer(FFullBitmap.Height) then
                 Area.Rect.Height := Integer(FFullBitmap.Height) - Area.Rect.Y;
            Inc(X, AREA_SIZE);
        end;
        Inc(Y, AREA_SIZE);
    end;

    // Create all threads, but don't start them
    // Thread cannot be started because it would interfere with area allocation
    FAreaIndex := 0;
    for I := 1 to FThreadCount do begin
        NewThread                 := TMandelThread.Create(TRUE);
        NewThread.Area            := FAreas[FAreaIndex];
        NewThread.OnComputed      := MandelThreadComputed;
        NewThread.OnTerminate     := MandelThreadTerminate;
        NewThread.FreeOnTerminate := TRUE;
        FThread.Add(NewThread);
        Inc(FAreaIndex);
        if FAreaIndex >= FAreas.Count then
            break;
    end;

    // Set the counter pf to be colorized areas
    FColorizeCount := FAreas.Count;

    // Now start all thread, in reverse order. Reverse order is required
    // because threads may terminate and be removed from list, messing the
    // indexing.
    FStartTime := GetTickCount;
    for I := FThread.Count - 1 downto 0 do
        FThread[I].Start;
end;


// Warning: this is called in the context of the threads
procedure TMandelbrotExplorerForm.MandelThreadComputed(
    Sender        : TObject;
    const CurArea : TMandelArea;
    var   NewArea : TMandelArea);
begin
    if FTerminate then
        Exit;
    // We must pass the index instead of the pointer because the message
    // handling can be done much later when the area has been reallocated
    PostMessage(Handle, WM_COLORIZE, 0, CurArea.Index);
    FCritSect.Enter;
    if FAreaIndex < FAreas.Count then begin
        NewArea := FAreas[FAreaIndex];
        Inc(FAreaIndex);
    end;
    FCritSect.Leave;
end;


procedure TMandelbrotExplorerForm.MandelThreadTerminate(Sender : TObject);
begin
    // Simply remove the terminated thread from the thread list.
    FThread.Remove(Sender as TMandelThread);
end;

The FCritSect variable is very important. This is one of the synchronization mechanisms I talked above. A critical section works like this: only one thread at a time can execute the “Enter” method. Once the “Enter” method has been executed by a thread, any other thread calling “Enter” is made sleeping. When the “Leave” method is called, one and only one of the sleeping threads is awaken and continue execution. When this thread executes the “Leave” method, another thread is awaken and so forth.

A critical section MUST be used here because we increment FAreaIndex and use it to get the next area for the thread calling MandeThreadComputed.

Another part of the code requires some explanation. A flag “FTerminate” is used to signal the user wants to terminate the current computing. It is set my MandelCreateImage itself when called before all threads are done.

Since we cannot stop the thread immediately (It takes some time to stop a thread), we use another custom message WM_TERMINATING. The message handler will check if all thread are done. If not, it sleeps 0.25 sec and then post the message again. If all threads are done, it calls MandelCreateImage which will start a new image creation.

Here the message handler code:

procedure TMandelbrotExplorerForm.WMTerminating(var Msg: TMessage);
var
    TmpMsg : TMsg;
begin
    if FThread.Count <= 0 then begin
        // No more threads are computing.
        // Remove any WM_COLORIZE from message queue
        while PeekMessage(TmpMsg, Handle, WM_COLORIZE, WM_COLORIZE, 1) do;
        FTerminate := FALSE;
        MandelCreateImage;
    end
    else begin
        Sleep(250);
        PostMessage(Handle, WM_TERMINATING, 0, 0);
    end;
end;

The final word

I hope you enjoyed reading this article. All in all, the code is fairly simple. Actually the code for the user interface is longer!

If you are interested by the source code (Delphi XE5), just drop me a private email.

References:

Parallel computing: http://en.wikipedia.org/wiki/Parallel_computing
Multithreading: http://en.wikipedia.org/wiki/Multithreading_(software)#Multithreading
Synchronization objects: http://msdn.microsoft.com/en-us/library/windows/desktop/ms686364(v=vs.85).aspx
Mandelbrot set: http://en.wikipedia.org/wiki/Mandelbrot_set
GDI+: http://msdn.microsoft.com/en-us/library/windows/desktop/ms533798(v=vs.85).aspx
GDI+ for Delphi : http://www.bilsen.com/gdiplus


Follow me on Twitter
Follow me on LinkedIn
Follow me on Google+
Visit my website: http://www.overbyte.be
This article is available from http://francois-piette.blogspot.be